- Quelle est la durée de propagation d’un signal dans un filtre ? Quelle est l’efficacité du blindage d’un composant ? Qu’elle est la permittivité relative d’un substrat micro ruban ? Quelles sont les performances d’un absorbeur d’ondes radar ?
- Répondre à ces questions nécessite de connaître les caractéristiques diélectriques et magnétiques des matériaux aux fréquences RF et micro-ondes.
- Un analyseur de réseau vectoriel permet de caractériser un matériau sous test (MUT pour Material Under Test) souvent de façon non destructrice et parfois sans contact.
- Anritsu présente dans cet article plusieurs techniques de mesure classiquement réalisées avec un analyseur de réseau vectoriel ainsi que quelques exemples concrets.
Auteur : Enrico Brinciotti, PhD, ingénieur en développement d’affaires, Anritsu – Région EMEA
Plusieurs méthodes de mesures ont été développées au fil des ans pour caractériser les propriétés diélectriques des matériaux : avec sonde coaxiale à extrémité ouverte (circuit ouvert), mesure en espace libre, résonateurs, et méthodes avec ligne de transmission.
Chaque technique possède son propre champ d’application dépendant de plusieurs facteurs tels que la fréquence propre de l’application, la précision requise pour la mesure, les propriétés isotropes et d’homogénéité, la forme du matériau (poudre, liquide ou solide), sa taille, les exigences en termes de test non destructif ou sans contact, et la plage de température.
Un analyseur de réseau vectoriel ou VNA (Vector Network Analyzer) permet de caractériser précisément et quantitativement les propriétés des matériaux, telles que la permittivité électrique et la perméabilité magnétique à des fréquences allant de quelques kHz à plusieurs THz.
Différentes méthodes asssurent l’extraction de la permittivité et la perméabilité du matériau sous test à partir de la mesure des paramètres S sur 2 ports ou 1 port. Les matériaux sous test peuvent être des matières biologiques et liquides jusqu’aux solides, y compris les poudres.
Propriétés diélectriques des matériaux
Les matériaux peuvent être classés en trois catégories : isolants (diélectriques), conducteurs et semi-conducteurs. Quand un matériaux diélectrique est exposé à un champ électrique externe, il est polarisé. La quantité d’énergie électromagnétique qu’un matériau emmagasine et dissipe est mesurée par ses propriétés diélectriques et magnétiques, appelées respectivement la permittivité électrique et la perméabilité magnétique. Toutes deux représentent des quantités complexes. La part réelle de la permittivité est souvent référencée comme étant la constante diélectrique. Les matériaux peuvent être divisés en deux catégories, dispersifs et non dispersifs, selon que leur permittivité change en fonction de la fréquence ou non (respectivement). Pour les matériaux dispersifs, il est nécessaire de quantifier leur comportement en fréquence. C’est pourquoi la permittivité est généralement mesurée par rapport à la fréquence. La permittivité relative complexe, notée εr, est définie comme suit :
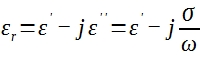
Où 
est la conductivité électrique (S/m), 
est l’unité imaginaire, et 
est la fréquence angulaire (rad/s). La permittivité complexe 
consiste donc en une partie réelle et en une partie imaginaire. La partie réelle 
mesure la quantité d’énergie stockée dans le matériau, tandis que la partie imaginaire 
, également connue sous le nom de facteur de perte, mesure la quantité d’énergie perdue par le matériau. Le rapport entre la partie imaginaire et la partie réelle de la permittivité complexe est défini comme la tangente de l’angle de pertes (facteur de dissipation ou facteur de perte).
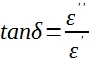
Elle mesure la dissipation inhérente d’énergie électromagnétique émise par le matériau sous test (MUT).
Techniques de mesure de matériaux à l’aide d’un VNA
Plusieurs méthodes utilisant un analyseur de réseau vectoriel existent. Elles permettent de mesurer les propriétés électriques des matériaux, soit la permittivité électrique ε et la perméabilité magnétique µ, depuis quelques kHz jusqu’aux THz. À partir des mesures des paramètres S complexes, la partie réelle et la partie imaginaire de ε et µ peut être obtenue, simultanément. Quatre techniques peuvent être définies : les méthodes avec sonde coaxiale à extrémité ouverte, les méthodes avec ligne de transmission, les techniques de mesure en espace libre, et les résonateurs. Les propriétés diélectriques du matériau sous test (MUT) dépendent, entre autres, de la fréquence, de l’anisotropie, de l’homogénéité et de la température. En conséquence, il n’existe aucune meilleure technique qui ne permette de mesurer avec précision les propriétés diélectriques de tous les matériaux que celle de les mesurer à toutes les fréquences et à toutes les températures. La meilleure méthode dépend de : la fréquence, la température, le régime de pertes, la forme du matériau sous test (en poudre, solide, liquide, etc.), sa taille (film mince, grand panneau, etc.), la nécessité de tests non destructifs et la possibilité de contact avec le matériau sous test ou non. Vous trouverez ci-après un résumé des quatre méthodes les plus couramment utilisées pour tester les propriétés des matériaux à des fréquences RF et micro-ondes.
Sonde coaxiale à extrémité ouverte
On utilise une sonde coaxiale à extrémité ouverte pour mesurer les matériaux avec pertes à de hautes fréquences sur une large plage de fréquences allant de 0,5 GHz à 110 GHz. Les propriétés diélectriques sont extraites des mesures de réflexion à 1 port à l’aide d’une sonde métallique plaquée contre le matériau sous test. Une étape d’étalonnage est nécessaire, qui sert de référence pour le signal réfléchi mesuré dans le plan d’ouverture de la sonde. Les solides plats et les liquides constituent des échantillons bien adaptés à cette technique. Pour les matériaux dotés d’une faible permittivité, la méthode introduit des incertitudes et des erreurs.
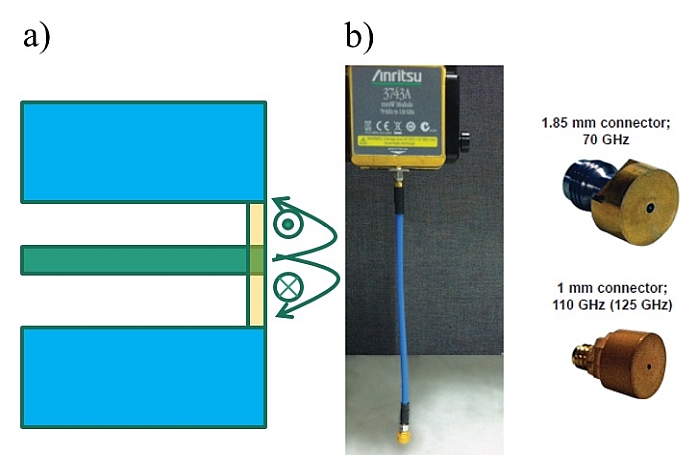
Méthode avec ligne de transmission
Dans la méthode avec ligne de transmission, le matériau à caractériser est placé dans une ligne de transmission (par exemple, une guide d’onde ou un câble coaxial). La permittivité et la perméabilité sont extraites à partir des paramètres S des mesures en transmission et en réflexion. La méthode peut être appliquée aussi bien à des solides qu’à des fluides. Elle induit une meilleure précision et une meilleure sensibilité que la technique de la sonde coaxiale à extrémité ouverte. Le taux d’erreur est inférieur à 5 % pour la permittivité et la perméabilité et, à des niveaux de pertes relativement élevés, il est inférieur à 10 % pour la mesure de la tangente de l’angle de pertes. La résolution de la tangente de l’angle de pertes est de ±0,01. Par conséquent, les matériaux avec une tanδ < 0,01 ne peuvent pas être caractérisés.
Montages en espace libre
Sur les montages en espace libre, les paramètres S sont calculés entre deux antennes avec l’échantillon placé sur une ligne droite. À partir de l’analyse des coefficients de transmission et de réflexion d’une onde électromagnétique (EM) qui se propage depuis l’espace libre dans l’échantillon, les propriétés diélectriques du matériau sous test peuvent être extraites. L’antenne cornet émettrice envoie un faisceau gaussien collimaté au travers de lentilles diélectriques, limitant ainsi les contributions à la diffraction sur la périphérie du matériau analysé. Les sources d’erreur communes sont le mauvais alignements de la sonde/de l’échantillon, ainsi que les effets de diffraction. La fabrication et l’alignement des lentilles doivent être très précis afin de limiter les aberrations du front d’onde et les réflexions multiples. En conséquence, les montages en espace libre, en particulier pour les applications à large bande, s’avèrent relativement chers. La précision nette et la résolution des pertes sont similaires à celles relevées pour la méthode avec ligne de transmission.
Légendes figure 3 :
Through >>> Calibrage Through (en ligne directe)
Reflect standard >>> Calibrage en Reflexion
Match standard >>> Calibrage avec une charge adaptée
MUT measurement >>> Mesure d’un materiau sous test
Résonateurs
Les méthodes résonantes permettent l’extraction des propriétés diélectriques à une seule fréquence ou à un ensemble de fréquences discrètes. On peut ainsi atteindre une plus grande précision (par exemple à 4 chiffres pour la permittivité et la tangente de l’angle de pertes) et sensibilité par rapport aux méthodes décrites ci-dessus. Le matériau sous test est placé à l’intérieur d’une cavité résonante, en connaissant au préalable la fréquence de résonance et le facteur de qualité. Le changement de ces deux valeurs quand le matériau sous test est introduit est mesuré, à partir duquel la permittivité et la perméabilité sont déterminées. Le taux d’erreur est inférieur à 1 % pour la permittivité et à 0,3 % pour la tangente de l’angle de pertes. La précision n’est pas aussi bonne pour les matériaux avec pertes élevées, car le pic résonnant s’élargit à mesure que les pertes augmentent.
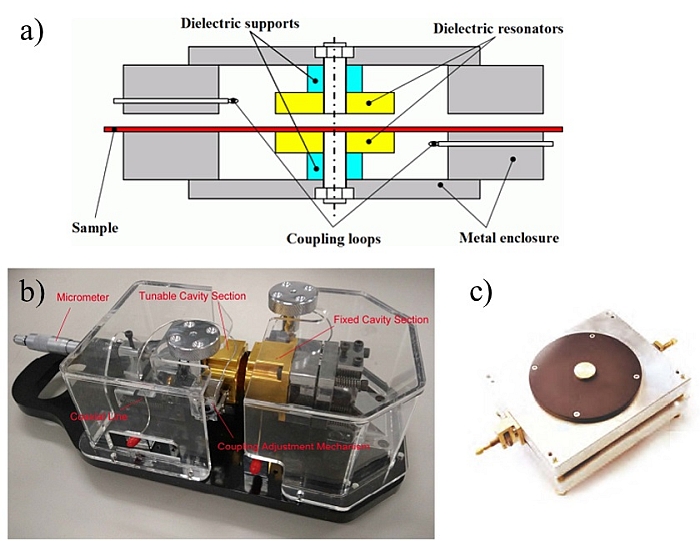
Légendes figure 4 :
a) Dielectric supports >>> Supports du diélectrique
Dielectric resonators >>> Résonateurs diélectriques
Sample >>> Échantillon
Coupling loops >>> Boucles de couplage
Metal enclosure >>> Boîtier métallique
b) Micrometer >>> Micromètre
Tunable cavity section >>> Section de cavité réglable
Fixed cavity section >>> Section de cavité fixe
Coaxial line >>> Ligne coaxiale
Coupling adjustment mechanism >>> Mécanisme d’ajustement du couplage
Comparaison des différentes méthodes
Chaque technique possède son propre champ d’applicabilité. Le choix dépendra notamment de : la plage de fréquences concernée, la précision requise pour la mesure, les propriétés isotopes et d’homogénéité, la forme du matériau (c’est-à-dire en poudre, liquide ou solide), sa taille, les exigences en termes de test non destructif ou sans contact, et enfin la plage de température. Le tableau ci-dessous résume les avantages, les champs d’application et les limites de chaque technique.
|
Techniques de mesure |
Matériaux |
Paramètres S |
Propriétés diélectriques |
Capacités et limites |
|
Sonde coaxiale à extrémité ouverte |
|
S11 |
|
|
|
Ligne de transmission |
|
S11 , S21 |
, µr |
|
|
En espace libre |
|
S11 , S21 |
, µr |
|
|
Méthode résonante (cavité) |
|
Fréquence de résonance, Facteur Q |
, µr |
|
