- Dans les systèmes de communication modernes, l’information est numérisée, codée à des niveaux logiques de 1 et de 0, et souvent encodée par la suite selon des schémas de modulation complexes comme la modulation d’amplitude d’impulsion (PAM, Pulse Amplitude Modulation) ou la modulation d’amplitude en quadrature (QAM, Quadrature Amplitude Modulation).
- L’intégrité des informations du côté du récepteur peut être critique, c’est pourquoi il est essentiel que toutes les erreurs puissent être évitées, ou à défaut corrigées.
- Lorsque des erreurs importantes se produisent dans les données transmises, de telle sorte que des portions significatives des données sont manquantes, ou que la trame est très différente de ce qui est attendu, des systèmes de gestion des équipements peuvent déterminer le problème et le résoudre de la manière adéquate. En cas d’erreur mineure, cependant, lorsque seul un petit nombre de bits dans la trame est corrompu, l’aspect des données a l’air identique pour le système ce qui fait que les erreurs sont donc difficilement repérées. Pourtant, une seule erreur suffit pour entraîner une modification drastique du message, alors que le système n’a aucun moyen de s’en rendre compte.
- Cet article, proposé par Anritsu, présente la correction d’erreur sans voie de retour (ou FEC, pour Forward Error Correction), une fonction capable de corriger les erreurs dans les données reçues, les circonstances de son apparition ainsi que certains des avantages et des inconvénients de son utilisation.
Andy Cole, Anritsu EMEA
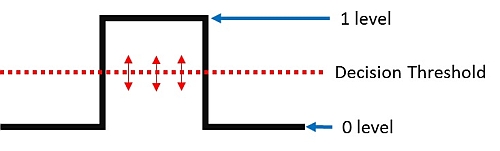
1 Level > Niveau 1 – Decision Threshold > Seuil de décision – 0 Level > Niveau 0
Le schéma montre la transition de tension entre le niveau logique 0 et le niveau logique 1, puis le retour à l’état logique 0. À un certain niveau de tension, quelque part entre l’état logique 0 et l’état logique 1, il existe un seuil au niveau duquel une décision électronique est prise quant à savoir s’il s’agira d’un 0 ou d’un 1 à ce point précis du flux de données. Ainsi, si l’amplitude du bit n’est pas suffisamment au-dessus ou en-dessous de ce seuil, cela peut entraîner une erreur d’interprétation des données. L’atténuation du signal, la gigue et le bruit dans le système peuvent facilement entraîner des erreurs.
Bits de parité
Les bits de parité offrent l’un des moyens les plus simples pour vérifier qu’un bloc de données reçu présente une erreur de bits. On compte le nombre de logiques 1 et on envoie un bit de parité en même temps que les données.
La parité peut être paire ou impaire ; ici, supposons qu’il s’agisse d’une parité impaire. Si l’on envoie un mot de données 11101001, on compte cinq « 1 » dans le mot. Le chiffre cinq étant un chiffre impair, il est défini comme étant une parité impaire ; on ajoute donc un bit de parité 0 à la fin du train de bits. Si le nombre de logiques « 1 » avait été pair, qui diffère de la parité impaire, alors on aurait ajouté un bit de parité « 1 » à la fin du train de bits.
Au niveau du récepteur, on applique simplement le même calcul au mot de données et on vérifie que le bit de parité reçu correspond bien au bit de parité envoyé.
Comme les bits sont binaires et ne possèdent que deux états, la moindre erreur de bit fera basculer le bit de parité de 0 à 1 et vice versa. Cependant, si le mot de données comporte deux erreurs, ou tout autre nombre d’erreurs pair, alors le calcul de parité est faussé. C’est pourquoi la parité ne s’avère utile que lorsque les erreurs sont très improbables et que, si elles se produisent, seul un bit est susceptible de se retrouver erroné dans les données reçues. Si les données sont critiques, la seule action possible quand la parité n’est pas confirmée consiste à renvoyer les données. Il serait bien plus utile, une fois une erreur identifiée, d’avoir une solution pour la corriger. C’est exactement ce que permet la correction d’erreur sans voie de retour (FEC, Forward Error Correction).
Correction d’erreur sans voie de retour (FEC)
La correction d’erreur sans voie de retour est un procédé dans lequel les résultats des algorithmes sont envoyés comme information supplémentaire avec les données depuis l’émetteur. En répétant les mêmes algorithmes à l’autre extrémité, le récepteur a la possibilité de détecter les erreurs au bit près et de les corriger (erreurs corrigibles) sans devoir renvoyer les données.
Le code de Hamming, sans doute la première forme de FEC, fut inventé par Richard Hamming dès 1950. Travaillant alors pour les laboratoires Bell, il était frustré par les erreurs fréquentes dans les cartes perforées utilisées pour enregistrer et transférer les données en même temps. Il inventa alors une méthode codée permettant d’identifier et de corriger les erreurs, évitant de devoir reproduire et renvoyer les cartes perforées en cas d’erreur.
Dans l’exemple suivant, un mot de 8 bits est envoyé, suivi de cinq bits de contrôle. Si une erreur survient sur l’un des bits, l’erreur peut être détectée et même corrigée. Supposons que l’on veuille envoyer le mot de données 11101001.
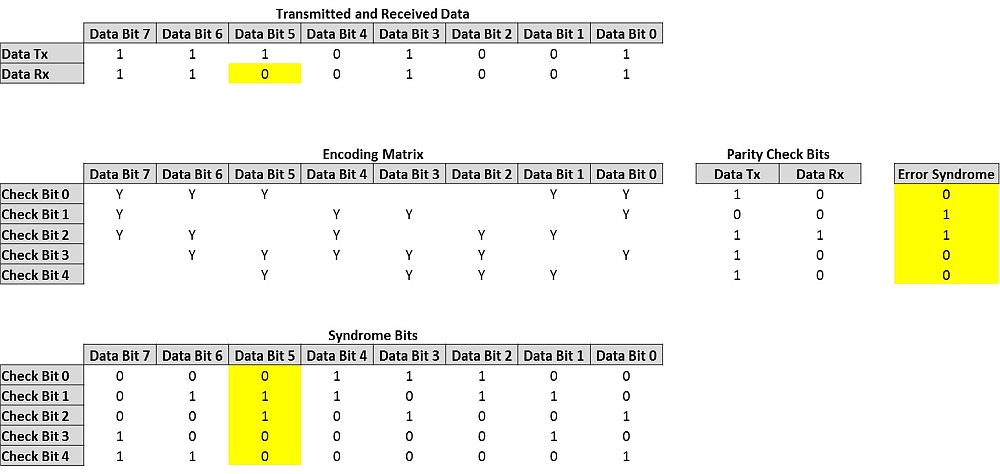
Figure 2. Principe de base du fonctionnement du code de Hamming.
Transmitted and received Data > Données envoyées et reçues
Data Tx > Données Tx
Data Rx > Données Rx
Data Bit 7 > Bit de données N°7
Encoding Matrix > Matrice d’encodage
Check Bit 0 > Bit de contrôle 0
Parity Check Bits > Bits de contrôle de parité
Error Syndrome > Syndrome d’erreur
Syndrome Bits > Bits de syndrome
D’abord, cinq bits de contrôle, qui seront ajoutés au mot de données, sont calculés. On compte le nombre de « 1 » dans le flux de données qui correspondent aux « Y » dans la rangée « bit de contrôle 0 » de la matrice d’encodage, pour calculer la valeur du premier bit de contrôle de parité. On répète le même processus pour les rangées « Bit de contrôle 1 » à « Bit de contrôle 4 », pour calculer le reste des bits de contrôle de parité pour les données émises (Tx). Dans l’exemple ci-dessus, les bits de contrôle étant 10111, le mot 1110100110111 est donc transmis.
Le récepteur effectue la même vérification sur les mots de huit bits et compare les deux séries de bits de contrôle de parité, un bit à la fois. Si les bits de contrôle de parité sont identiques, cela donne un « 1 », si la valeur diffère, cela donne un « 0 ». Si le résultat est uniquement constitué de 1, les données ne comportent pas d’erreur. Si au contraire il comporte autre chose, on est sûr qu’il y a une erreur. Ce cas de figure est dénommé « syndrome », souvent utilisé dans les expressions « décodage par syndrome », « erreur de syndrome », etc.
Dans l’exemple ci-dessus, le « Bit de données N°5 » est reçu avec une erreur (un 0 au lieu d’un 1), entraînant une erreur de syndrome 01100. La matrice des « Bits de syndrome », qui correspond à la matrice d’encodage, confirme que l’erreur se situe sur le Bit de données N°5. Le système peut à présent inverser son état afin que les données soient corrigées.
Au fil des années, la correction d’erreurs de codage a continué à être développée au point que dorénavant de nombreux bits erronés dans un long flux de données peuvent être détectés et corrigés avec succès au niveau du récepteur, sans avoir besoin de renvoyer les données.
Code correcteur de Reed Solomon (RS-FEC)
La norme G.709 définit un code correcteur Reed Solomon (RS-FEC) pour les réseaux de transport optique actuels (OTN, Optical Transport Network). Cette norme permet également aux fournisseurs d’équipements d’utiliser un code correcteur supplémentaire pour améliorer l’efficacité de la correction d’erreur.
Parfois désigné sous le nom de code RS (255,239), le correcteur d’erreur FEC basé sur le code de Reed Solomon utilisé pour les réseaux OTN gère et corrige les erreurs de données pour un bloc d’information de 239 symboles, chaque symbole étant composé de 8 bits. Un ensemble de 16 autres symboles, chacun codé sur 8 bits, est utilisé pour transmettre le résultat des algorithmes RS-FEC, portant la taille totale du bloc de données transmis à 255 symboles. Environ 6 % des données transmises correspond au surcoût du code correcteur FEC. Ainsi, vous vous demandez sans doute pourquoi, alors que son coût est si élevé, ce code correcteur est-il si efficace et fournit-il une solution si parfaite pour la correction d’erreur ?
Pour garantir une transmission sans erreur sans FEC, il convient de maintenir un bon rapport signal sur bruit (SNR, Signal to Noise Ratio), pour lequel l’amplitude du signal est bien au-dessus du bruit électrique (le plancher du bruit) du système. Plus le signal s’atténue, plus il est proche du bruit, augmentant la probabilité que le bruit cause des erreurs dans les données. Le maintien de la puissance optique au niveau nécessaire pour éviter les erreurs peut nécessiter d’amplifier le signal, éventuellement en convertissant le signal en électricité, en l’amplifiant et en le renvoyant sous forme de signal optique, ce qui se traduit par des coûts supplémentaires et par une latence plus élevée.
Cependant, parce que la FEC peut corriger un certain nombre de bits erronés, on peut accepter une réduction du niveau du signal et le laisser chuter proche du niveau du bruit, du moment qu’on reste dans la limite des erreurs corrigibles. Cette réduction autorisée du SNR s’appelle le gain de codage, défini comme la différence de SNR en entrée par rapport à un taux d’erreur bit « BER » de sortie donné (BER, Bit Error Rate). Le SNR en entrée est mesuré soit comme facteur Q soit comme rapport Eb/N0 (rapport énergie par bit sur densité spectrale de bruit).
Le graphique ci-dessous montre qu’un système nécessitant un taux d’erreur BER de 10-15 RS-FEC fournit un gain de codage d’environ 6,2 dB. Cependant, lorsqu’un code correcteur additionnel provenant du fournisseur d’équipements est mis en œuvre, on peut atteindre un gain de codage avoisinant les 12 dB.
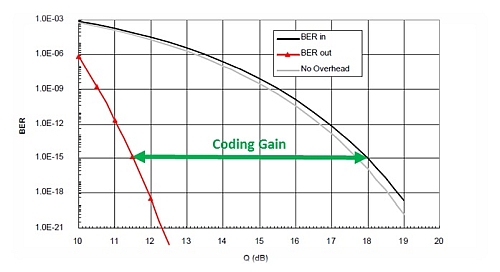
BER in > BER en entrée
BER out > BER en sortie
No Overhead > Pas de surplus de données
Coding Gain > Gain de codage
Le gain de codage offre plusieurs avantages qui améliorent l’efficacité de l’équipement réseau, entraînant une meilleure utilisation de la bande passante. Parmi ces avantages, on peut citer :
- La capacité à diminuer la puissance de transmission et à maintenir l’intégrité de l’information sur l’ensemble de la portée.
- La capacité à transmettre des signaux plus loin sans avoir besoin de les amplifier ou de les renvoyer, améliorant l’efficacité de l’équipement réseau, la puissance et la latence.
- La réduction des besoins en équipements réseau et en puissance, entraînant des économies grâce à un moindre recours à la surveillance environnementale (bâtiments, climatiseurs, etc.).
- Si le nombre de canaux DWDM est limité par la puissance agrégée, la capacité à réduire la puissance de transmission permet davantage de canaux avant d’atteindre la puissance agrégée maximale.
Vérification FEC
La correction FEC est étroitement liée au maintien de l’intégrité des données sur les systèmes de communication modernes, afin de tirer le meilleur parti de ces avantages et améliorations en termes d’efficacité de l’équipement réseau, de bande passante et de considérations environnementales. La correction FEC doit être solide et fiable. C’est pourquoi il est nécessaire de vérifier que le code correcteur fonctionne selon les spécifications de la norme G.709 et, dans le cas d’un code correcteur supplémentaire, selon les spécifications plus contraignantes du fournisseur de l’équipement.
Le testeur de réseau « Network Master Pro » d’Anritsu répond aux besoins professionnel d’une recette complète de tests. Il caractérise les performances du réseau et teste l’efficacité de la correction d’erreur FEC mise en œuvre.
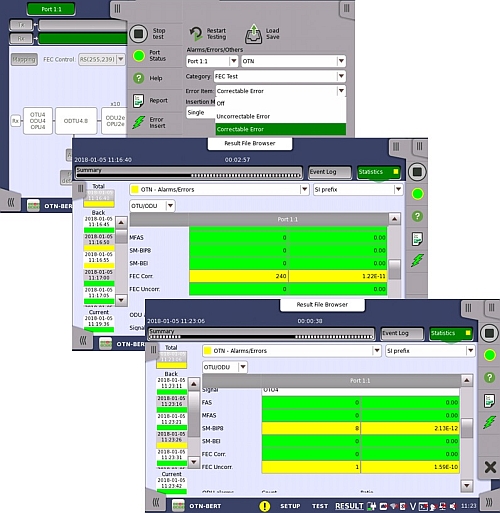
L’image ci-dessus montre comment les erreurs FEC peuvent être simulées par le Network Master Pro ainsi que la facilité de lecture des écrans de résultats qui fournissent des données statistiques sur la façon dont l’équipement réseau gère les erreurs FEC corrigibles et non corrigibles.
En conclusion, malgré un surplus de données nécessaire conséquent de 6 %, les avantages de la correction FEC dépassent largement les coûts. La réduction du besoin en puissance optique du canal via un gain de codage de 6,2 dB pour RS-FEC, et un gain de codage potentiel de 12 dB lorsqu’un code correcteur spécifique à un fournisseur est ajouté, résultent en des économies d’énergie grâce à une amplification et à une surveillance environnementale réduites, ainsi qu’en une meilleure utilisation du spectre utilisant davantage de canaux WDM pour gagner en bande passante. Mais l’équilibre est précaire entre le maintien de l’intégrité de l’information et l’apparition d’erreurs catastrophiques. C’est pourquoi, tester correctement le fonctionnement de la correction d’erreur FEC, en simulant des erreurs pour garantir que les erreurs sont corrigées et s’assurer que le taux d’erreur BER est atteint, est plus important que jamais.









