- Le nombre effectif de bits (ENOB pour effective number of bits) est un moyen de quantifier la qualité d’une conversion analogique-numérique.
- Un ENOB élevé signifie que les niveaux de tension enregistrés lors d’une conversion analogique-numérique sont de plus grande précision.
- Concernant une numérisation réalisée avec un oscilloscope, l’ENOB n’est pas seulement déterminé par la qualité du convertisseur analogique-numérique mais par le processus d’acquisition, de numérisation et de traitement dans son ensemble.
- Dans cette note d’application, Rohde&Schwarz détaille les notions de base permettant de mesurer l’ENOB d’un oscilloscope.
# Convertisseur analogique-numérique idéal
La figure ci-dessous illustre le schéma d’un convertisseur analogique-numérique idéal (ADC pour analog to digital converter).
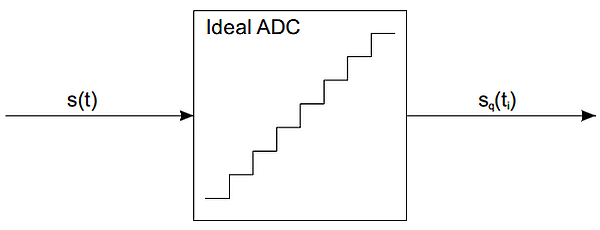
Le convertisseur analogique-numérique idéal est parfaitement linéaire et quantifie simplement le signal entrant. Le processus de quantification introduit un bruit de quantification. A partir de la puissance du signal et la puissance du bruit, il est possible de calculer le rapport signal sur bruit (SNR pour signal to noise ratio) après la conversion analogique/numérique. Si une onde sinusoïdale pleine échelle est utilisée comme signal d’entrée, alors le rapport signal-bruit peut être obtenu par l’équation suivante :
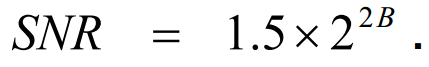
B désigne le nombre de bits de l’ADC.
L’expression en dB du SNR est fournie par l’équation :
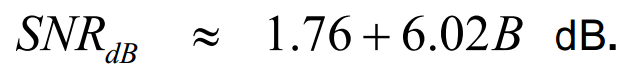
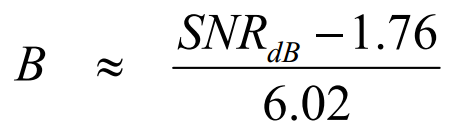
Cette équation montre comment le nombre de bits peut être obtenu à partir du rapport signal/bruit et constitue la base de calcul de l’ENOB. Dans le cas d’ADC idéaux, le résultat pour B sera toujours un entier réel positif. Dans le cas contraire, qui
sera examiné dans la section suivante, B peut être n’importe quel nombre réel positif.
# Convertisseur analogique-numérique non idéal
Les ADC idéaux n’existent pas. Chaque ADC ajoute quelques distorsions au signal d’entrée. Les distorsions typiques sont le bruit, une caractéristique d’entrée non linéaire ainsi que les erreurs de gain et d’offset (décalage). La figure 2 représente un modèle d’ADC non idéal.
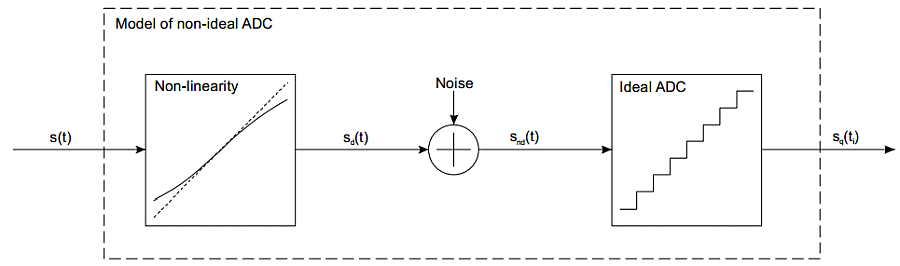
Le bruit contribue directement à une dégradation du SNR de l’ADC. Une non-linéarité se traduit par des harmoniques qui réduisent également le rapport signal-bruit obtenu. Ainsi, un ADC de 12 bits peut être spécifié avec un ENOB de 10,5. Cela signifie que même si l’ADC numérise le signal sur 12 bits, le SNR obtenu correspond à celui d’un ADC idéal de 10,5 bits.
Selon la conception de l’ADC, l’ENOB peut également dépendre de la fréquence d’entrée. Les hautes fréquences peuvent entraîner des non-linéarités plus importantes au sein du circuit, dégradant ainsi l’ENOB. Ainsi, une spécification détaillée d’un ADC comprend habituellement la variation de l’ENOB en fonction de la fréquence d’entrée.
# Étage d’entrée d’un oscilloscope
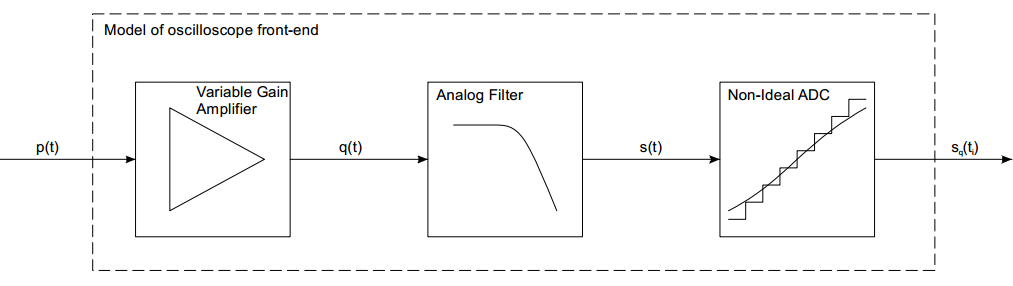
Dans un oscilloscope, des circuits complémentaires doivent être placés en entrée devant l’ADC afin d’en tirer le meilleur parti. Ces éléments sont représentés schématiquement sur la figure 3. Le premier élément est un amplificateur à gain variable (VGA pour variable gain amplifier), qui met à l’échelle le signal d’entrée de l’oscilloscope pour utiliser de manière optimale la plage dynamique de l’ADC. Le second est un filtre anti-repliement passe-bas. Ces deux éléments introduisent d’autres distorsions sur les signaux d’entrée. Le VGA, constitué de composants actifs, introduit des non-linéarités et présente un comportement dépendant de la fréquence. Le filtre analogique est moins critique, mais sa réponse en fréquence n’est pas idéale. Une conception appropriée de l’étage d’entrée doit minimiser les impacts négatifs sur le signal d’entrée.
# Mesure de l’ENOB
L’IEEE a défini la terminologie et les méthodes de test pour les convertisseurs analogique-numérique [1] : IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters, IEEE Standard 1241-2010. Voici sa définition de l’ENOB :
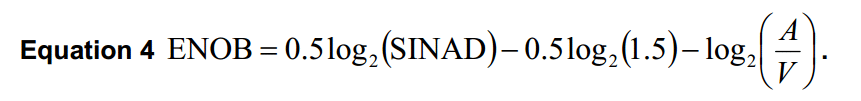
V : plage pleine échelle de l’appareil sous test.
A : amplitude crête à crête de l’onde sinusoïdale ajustée à la sortie.
SINAD : Signal-to-noise and distortion ratio pour Rapport signal/bruit et rapport de distorsion
Dans le présent document, le SINAD est défini par l’équation suivante :
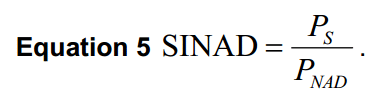
Ps : puissance du signal ; puissance dans l’intervalle de fréquences FFT (bin) correspondant à la fréquence d’entrée
PNAD : puissance de bruit et de distorsion ; somme des puissances dans tous les autres groupes de fréquences
à l’exclusion de l’intervalle de fréquence 0, jusqu’à et y compris l’intervalle de fréquence FFT correspondant à la fréquence de Nyquist.
Il est à noter ici que le SNR et le SINAD, tels que définis dans la terminologie IEEE [1], sont des rapports de valeurs efficaces et non des rapports de valeurs de puissance, ce qui est par exemple typique de l’ingénierie des communications. Dans le présent document, nous utilisons systématiquement les rapports des valeurs de puissance pour les deux mesures.
Dans la source [1], les méthodes de calcul du SINAD utilisant un domaine temporel ou une analyse du domaine fréquentiel sont définies. Par souci de simplicité, le présent document est axé sur le domaine de l’analyse de fréquences. Le choix de la fréquence de test approprié est décrit ultérieurement. Une transformée de Fourier rapide (FFT) est ensuite utilisée pour calculer Ps et PNAD comme défini ci-dessus.
# Choix de l’amplitude
La norme IEEE ne spécifie pas d’amplitude d’entrée particulière pour la mesure ENOB. Selon la source [1], n’importe quelle amplitude d’entrée peut être utilisée, puisque la différence entre l’amplitude à pleine échelle et l’amplitude réelle du test est prise en compte dans la définition de l’ENOB (voir dernier terme dans l’équation 4).
Il existe deux possibilités pour traiter l’amplitude.
1. L’ENOB est spécifié pour une amplitude d’entrée particulière. Les spécifications communes sont l’ENOB à 90 % ou à 95 % de la pleine échelle. En utilisant la définition de l’équation 4, l’ENOB apparaîtra d’autant mieux que l’amplitude d’entrée est faible, car seules les non-linéarités jusqu’à l’amplitude de test influencent réellement la mesure.
2. La normalisation de l’amplitude dans l’équation 4 n’est pas prise en compte et la mesure de l’ENOB est basée uniquement sur le SINAD. Grâce à cette méthode, le point de fonctionnement optimal du système sous test peut être trouvé comme le meilleur compromis entre la puissance d’entrée et la distorsion par des non-linéarités. Étant donné que cette définition ne correspond pas à la définition de la définition officielle d’ENOB, il s’agit de l’ENOB*. Notez que l’ENOB* est la mesure la plus pratique pour la conception et le test de systèmes. Il correspond directement à la qualité du signal observé sur l’appareil de mesure. La mesure de l’ENOB permet de comparer différents systèmes, mais ne constitue une référence utile que si elle est citée avec l’amplitude d’entrée à laquelle l’ENOB a été mesurée.
# Choix de la fréquence
La fréquence d’entrée doit être choisie pour s’adapter exactement à un intervalle de fréquence de la FFT. Cela revient à dire que la séquence échantillonnée ne doit inclure que des périodes entières du signal d’essai. Ceci est important pour exclure tout effet de fenêtrage qui rendrait la mesure inutilement compliquée.
De plus, pour des mesures fiables, il faut échantillonner le plus grand nombre possible de phases du signal d’entrée et activer tous les codes de sortie de l’ADC. Selon la section 5.4.1 de la source [1], les fréquences d’essai optimales sont fournies par l’équation :
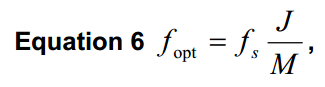
fopt : une fréquence d’essai utile pour le calcul de l’ENOB
fs : fréquence d’échantillonnage du dispositif sous test
M : nombre d’échantillons de la séquence de test
J : nombre de périodes de signal d’entrée dans la séquence de test. Ce devrait être un nombre entier qui est relativement amorcé à M. Le fait d’être relativement amorcé signifie qu’il n’y a pas de facteurs communs. Par exemple, 100 (facteurs 2 et 5) est relativement amorcé à 9 (facteur 3) mais pas à 15 (facteurs 3 et 5).
Dans les mesures suivantes, seules les fréquences qui peuvent être dérivées de l’équation 6 sont utilisées.
# Choix du nombre d’échantillons
Selon la source [1], une longueur de séquence minimale est spécifiée par l’équation suivante :
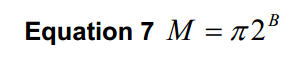
Cette condition assure une densité élevée de phases échantillonnées du signal de test et garantit ainsi des résultats fiables.









